Lösen Sie die folgenden Aufgaben.
Die nach oben geöffnete Normalparabel verläuft durch die Punkte und . Geben Sie die Funktionsgleichung von in der Normalform an.
Die Normalparabel ist nach unten geöffnet und hat denScheitelpunkt ). Geben Sie die Funktionsgleichung von in der Normalform an
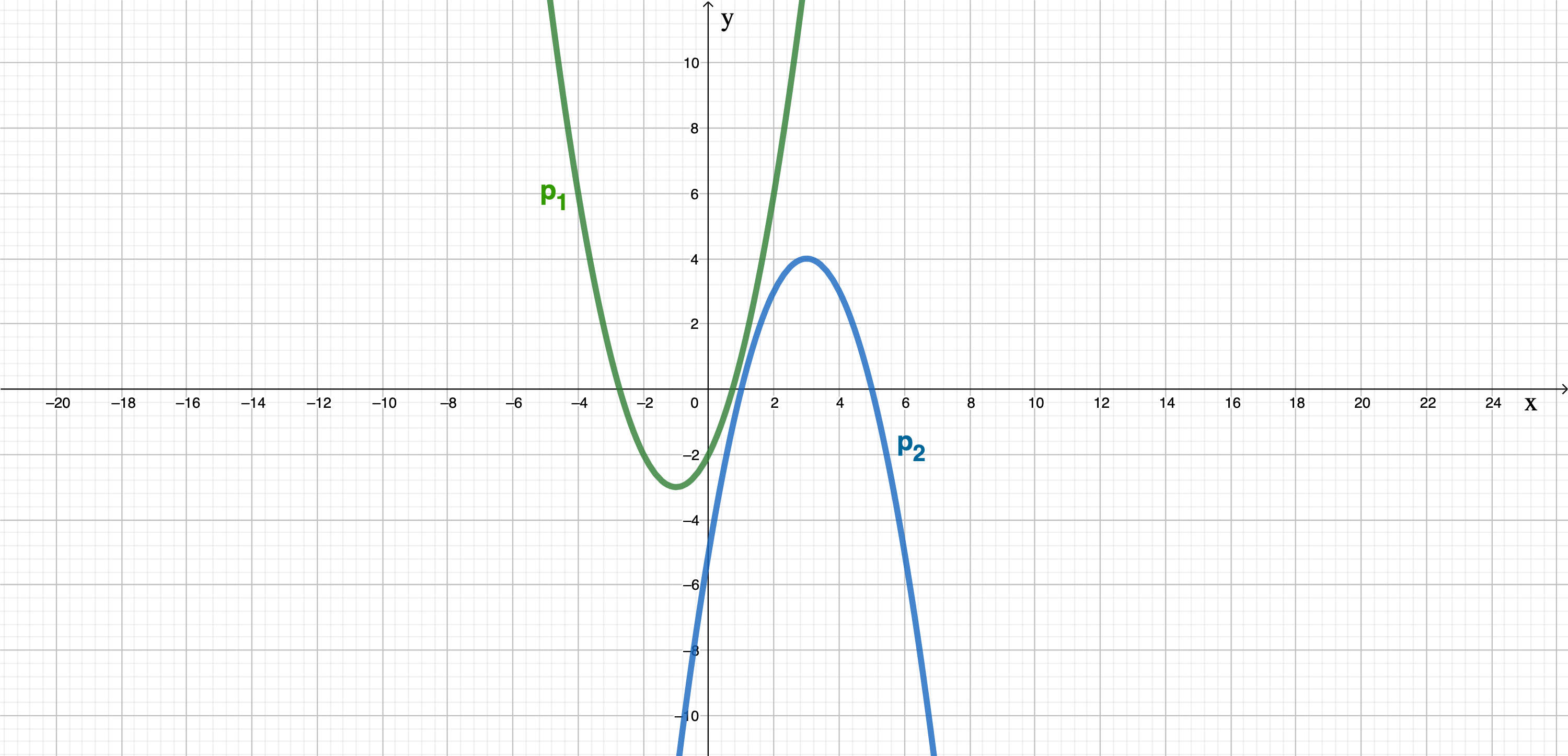
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der Längeneinheit 1 cm.
Der Punkt liegt auf der Normalparabel . Berechnen Sie die fehlende y-Koordinate.
Überprüfen Sie rechnerisch, ob der Punkt auf der Parabel liegt.
Bestimmen Sie durch Rechnung den Scheitelpunkt der Parabel .
Die Parabel schneidet die x-Achse in den Punkten und . Ermitteln Sie die x-Koordinaten von und rechnerisch.
Zeigen Sie rechnerisch, dass die Gerade keinen gemeinsamen Punkt mit der Parabel hat.